tayapeople.blogg.se - Babylonian numerals to mayan

This ambiguity is also why the calculator does not work with fractions, and can only divide when the result is an integer. Babylonian numerals (Languages), numerals Type the number of Babylonian numerals you want to convert in the text box, to see the results in the table.

It would be impossible to parse the input accurately without this system, as there could be several interpretations of the number entered. This is why the calculator above uses an additive system for input. Though large and small numbers could be represented, not having a symbol for zero left the number system with much ambiguity without context. Unlike our number system, the Babylonians represented numbers in base 60, so every number increases its value by a factor of 60 as you move left. The Babylonians used a positional number system, which allowed them to represent nearly any number, no matter how large or small.

Enter the next number into the second box just as you did the first.

Your number is displayed in base 60, just as the Babylonians wrote their numbers.

Enter a number in the first box by additively clicking on the 1 or the 10 symbol (e.g.

This makes for a confusing system, the details of which we will skip. Students learn about the Mayan Number System and use cards with the Mayan number symbols to assemble two-digit and three digit numbers in base 20. The days of the year were thought to be gods, so the formal symbols for the days were decorated heads, like the sample to the left Since the basic calendar was based on 360 days, the priestly numeral system used a mixed base system employing multiples of 20 and 360. For the priests, the number system was governed by ritual. Not only did these two systems use different symbols, they also used different base systems. There were two numeral systems developed by the Mayans-one for the common people and one for the priests. write a hindu-arabic numeral as a babylonian numeral (involves long division by a multiple of 60.if the given numeral is greater than 60-otherwise it is easy) 2 on study sheet keep dividing until the remainder is less than 60. Another important source of information on the Mayans is the writings of Father Diego de Landa, who went to Mexico as a missionary in 1549. In fact, much of what we know about this culture comes from their calendar records and astronomy data. The calendar, and calculations related to it, were thus very important to the ritual life of the priestly class, and hence the Mayan people. This class of priests developed a philosophy with time as divine and eternal. The Mayans had a sophisticated ritual system that was overseen by a priestly class. The Yucatan Peninsula (see figure 16 ) in Mexico was the scene for the development of one of the most advanced civilizations of the ancient world. Notice that changing a number from the Babylonian or Mayan numeration System to the Hindu-Arabic (or decimal or base 10) system involves multiplication. The Mayan civilization is generally dated from 1500 BCE to 1700 CE. See also: Code-Breaking overview Babylonian numerals Big number calculator Binary to decimal Decimal to binary Decimal to hex Euler number. The numerals are made up of three symbols, of which one denotes zero.

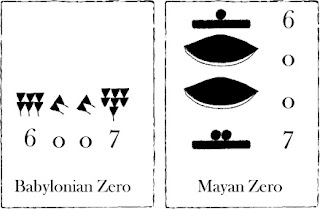
It was a vigesimal (base 20) number system. In this chapter, we wrap up with a specific example of a civilization that actually used a base system other than 10. Maya numerals was the number system of the Mayan civilization. The Babylonians used a base-sixty (sexigesimal) system. For example, the Natives of Queensland used a base-two system, counting as follows: “one, two, two and one, two two’s, much.” Some Modern South American Tribes have a base-five system counting in this way: “one, two, three, four, hand, hand and one, hand and two,” and so on. The Babylonians developed a number system with base 60 and the Maya with base 20. However, other civilizations have had a variety of bases other than ten. In part they used Base 60, the same number we see all around us in minutes, seconds, and degrees of a triangle or circle. Our own base-ten system probably arose from the fact that we have 10 fingers (including thumbs) on two hands. This third group is represented by the Maya, the Babylonian, and the Roman numerals. The Babylonians used this Base 10, but only in part. Use two different methods for converting numbers between basesĪs you might imagine, the development of a base system is an important step in making the counting process more efficient. To translate a Hindu-Arabic number into Mayan numerals, the number must be grouped into groups the size of each place value.Identify bases that have been used in number systems historically.Other types, mainly of historical interest, include Egyptian, Babylonian, Mayan, Greek, and Roman numerals. Arabic numerals (0-9) are the ones most commonly used today.

Become familiar with the history of positional number systems A numeral is a symbol used to represent a number.